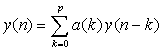
Non-parametric (conventional) spectral estimators such as the FFT or auto-correlation methods are limited in their resolving power, requiring long observation intervals in order to achieve acceptable accuracy and reduce leakage. For data sets of short duration, these conventional techniques are untenable, and an alternative approach is required. This has led to parametric (model based) spectral estimation, which has proven useful in extracting high resolution frequency spectra from relatively short data sets, providing the structure of the signal is known. The components of a known order related structure can be accurately tracked and extracted from a background of noise and components of an unknown structure.
The basic idea is that if y(t) depends on a finite set of parameters,
then all of its statistical properties can be expressed in terms
of , including its power spectrum Pxx(f) [SWAM95].
The most common and simplest of the parametric estimation techniques
is auto-regressive (AR) modelling of the signal. Auto-regressive
modelling consists of estimating the order of the coefficients
of , that when applied to the input signal will minimise the prediction-error
of the signal. Normally the minimisation criterion of the model
will be entropy based, which essentially maximises the random
nature of the error signal. The AR model of an input signal y(n)
can be represented as,
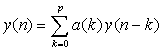
where p is the order of the model and a(k), k=1,2…p,
are the auto-regressive coefficients of the prediction process.
The error of the model is given by,
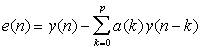
Non-Gaussian processes or processes that include coloured noise
can not be adequately modelled by its second order statistics,
motivating higher order parametric estimation techniques, such
as auto regressive moving average (ARMA) estimation. However studies
performed by C. K. Mechefske [MECH95] in regards to short time
sample for slowly rotating bearings, and E. Lopatinskaia [LOPA94b]
for the analysis of variable speed machinery indicate that AR
modelling of the vibration signal provides an adequate model.
Indeed, the additional information derived by ARMA modelling often
confuses the matter, and therefore complicates the diagnosis process.
Although AR and ARMA estimation have proven successful in analysing
signals of an evolutionary harmonic or broad band nature, the
problem of transient signal analysis can still not be adequately
addressed. Another mathematical model approach that has been highly
successful in analysing signals of an evolutionary harmonic nature
is adaptive Kalman filtering [LEUR94]. However, as with AR and
ARMA models, an accurate knowledge of the signals structure is
required before a reasonable model can be obtained.